100円時計の液晶ドライブ方法を解析
ダイソーでは見ませんが、他の100円ショップで売っている時計です。(1円玉は大きさのリファレンス)私の事ですから、別に時計が欲しかったわけではなくて、液晶部分だけ取って安い液晶表示器にならないか?ってことで、だいぶ前に買ってきてあったんですね。すでにばらして改造もしてあったので、電線が出ててワニ口クリップで電源供給してるのはご愛嬌って事で...
![]()
![]()
ということで、早速蓋を開けてみると表は左の写真のようになっていてアルカリボタン電池が1個入るようになってます。(前述の通り時計はバラシちゃってあったので、この写真は改造せずに実用に供している同じシリーズの温度計の中身です)表から止めているネジを外してやると基板の裏も見られるようになって、液晶の接続部は右の写真の様になってます。ピン数を数えてやると13ピンありました。時計用に3.5桁の液晶ですから、最初の1の2つに見えるセグメントは同じセグメントだとして、3桁 x 7 + 1 + 1(コロンの分)で23セグメントあるはずです。1本1本繋がっているにしてはピン数が足りないので、なんらかのマトリクスになっているようです。
液晶というと、ドライブ用のICが載ったものしか扱った事がないので、どういうドライブをすればいいのか全然わかってませんでした。検索して色々と調べてみると、どうやら極性を反転しながらACでドライブすると点くようです。ということで、まずはどんな風に動いてるのかをオシロで見せてもらいました。
![]()
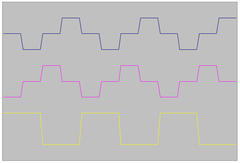
すると、こんな3種類の波形が観測されました。1ピンが一番上の波形で、13ピンが真ん中の波形、残りは一番下のような波形になっていました。32Hz位で動いているようです。電池のマイナス極を基準に上下が±1.5Vなので、チャージポンプかなんかで負電圧を発生させているようです。(Excelで作り直したので、立ち上がり立ち下がりが緩いですが、実際はもっと急峻です)おそらく1ピンと13ピンがコモンのピンでそれ以外がセグメントドライブのピンだってことは見当がつくんですが、これだけ見てても、なにがなにやらチンプンカンプンです。ただ順番によ〜くセグメントのピンを見ていくと、コロンが点滅するのに同期して方形波が階段波に対して位相がズレるように見えました。どうやらこれが鍵みたいです。
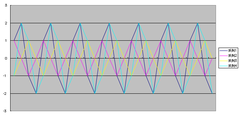
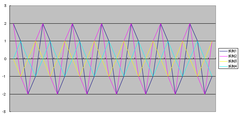
ということで、Excelで階段波形の中点の電位を表にして、方形波が取り得る4種類の位相状態と、1ピン、13ピンとの波形との引き算をグラフにしてみました。左が1ピンとの差、右が13ピンとの差です。(実際にはもっと階段状の波形になります)
![]()
これを見て初めてすごい事に気づきました。4ってことは2bitなので、2つの別のセグメントの4種類の状態を指定できるってことです。という視点で、系列を見ていくと、系列1は左のグラフで振幅2、右のグラフでも振幅2、系列2は左のグラフで振幅1、右のグラフでは振幅2、系列3は左のグラフで振幅1、右のグラフでも振幅1、系列4は左のグラフで振幅2、右のグラフでは振幅1です。振幅が2の時に点灯、振幅が1の時に消灯だと考えると、見事に2つのセグメントの状態を弁別できちゃうわけです。(本当の事を言うと最初位相は3種類だと間違っていたので迷路に入っていたのですが、階段波の周期を良く数えたら4つじゃんってのに気づいて、あ!!2bitじゃん!!これはもしかして!って4種類にしてグラフを作り直して実証できたのでした)
いやぁ、これがわかった時には大興奮でした。これを最初に考えた人アッタマ良い〜〜〜〜って、大感動でしたよ。Dallas semiconductor(今はMAXIM)の1-wireインターフェースのアドレス取得のプロトコル以来の感動だったかも。液晶のドライブを経験している人には当たり前じゃんってことなんでしょうけど、実に良くできてますよ。1.5Vの電池で6Vp-pの電圧掛けられてるし(実際3Vp-pでは消えてるわけだし)、色んな意味で実に良くできてます。
さて、ここまで解明できたんだから、あとは回路を組んでファームウェアをちょろちょろっと書けばセグメントとピンの対応はすぐに分かるだろうし、全て解決〜〜〜っと思いきや、良く考えてみるとちょっと変です。最初に書いたように23セグメントあるとすると、13ピンのうち2ピンがコモンですから、残りは11ピン。2 x 11 = 22で1セグメント分足りません。さてこれは困りました。そこで、7セグの表示でも数字だけに限れば、どこか常に同時に点滅するようなペアがあるんじゃないか?と思って7セグの数字パターンをメモ用紙に書いてみました。が、A〜Gまでのセグメントで常に同じように点滅する場所はどうも見当たりません。
 ここでまた新たなアハ体験が.... 時計なんで、10分の単位は0〜5までしかないじゃないですか。ここが鍵でした。0〜5までで考えると、AとDのセグメントは必ずAが点灯ならDも点灯、Aが消灯ならDも消灯という関係が保てています。他のペアは全滅なので、非常に稀な出来事なんですね。ということで、無事22セグメントで用が足りる事になりました。
ここでまた新たなアハ体験が.... 時計なんで、10分の単位は0〜5までしかないじゃないですか。ここが鍵でした。0〜5までで考えると、AとDのセグメントは必ずAが点灯ならDも点灯、Aが消灯ならDも消灯という関係が保てています。他のペアは全滅なので、非常に稀な出来事なんですね。ということで、無事22セグメントで用が足りる事になりました。
![]()
最後の仮説はまだ証明されていませんが、他に解は無いだろうと思うのでたぶん大丈夫でしょう。これで、とっても気分はスッキリです。が、同時に最初の目的に返ると困った事態です。下から2桁目が不自由な桁になってしまうので、7が表示できないんですよ。AをつけるとDもついちゃうので、7を表示させたかったら、アンダーラインがついた7みたいになるか、リみたいになるか、どちらかで我慢するしかありません。これも困ったもんですよねぇ。でも、もう一つ解を見つけました。CとGだけを点けて小っちゃい7ってことにするってのはどうでしょう?ちょっとかわいくなっちゃいますけど、アンダーラインやリよりはマシじゃないですかねぇ。だめかなぁ〜〜。:-)



最近のコメント